Адрес этой страницы изменился на http://www.nickolay.info/study/methods/05.html. Причины переезда
|
Pers.narod.ru. Обучение. Лекции по численным методам. Численное решение обыкновенных дифференциальных уравнений |
Численные методы решения задачи Коши для ОДУ первого порядка
Численные методы решения систем ОДУ первого порядка
Метод конечных разностей решения краевых задач для ОДУ
Многие задачи науки и техники сводятся к решению обыкновенных дифференциальных уравнений (ОДУ). ОДУ называются такие уравнения, которые содержат одну или несколько производных от искомой функции. В общем виде ОДУ можно записать следующим образом:
![]() , где x – независимая
переменная,
, где x – независимая
переменная, ![]() - i-ая производная от искомой функции. n -
порядок уравнения. Общее решение ОДУ n–го порядка
содержит n произвольных
постоянных
- i-ая производная от искомой функции. n -
порядок уравнения. Общее решение ОДУ n–го порядка
содержит n произвольных
постоянных ![]() , т.е.
общее решение имеет вид
, т.е.
общее решение имеет вид ![]() .
.
Для выделения единственного решения необходимо задать n дополнительных условий. В зависимости от способа задания дополнительных условий существуют два различных типа задач: задача Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.
Ясно, что при n=1 можно говорить только о задачи Коши.
Примеры постановки задачи Коши:

Примеры краевых задач:
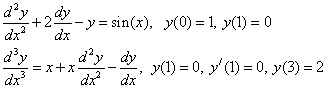
Решить такие задачи аналитически удается лишь для некоторых специальных типов уравнений.
Постановка задачи. Найти решение ОДУ первого порядка
![]() на отрезке
на отрезке ![]() при условии
при условии ![]()
При нахождении
приближенного решения будем считать, что вычисления проводятся с расчетным
шагом ![]() , расчетными
узлами служат точки
, расчетными
узлами служат точки ![]() промежутка
[x0, xn].
промежутка
[x0, xn].
Целью является построение таблицы
|
xi |
x0 |
x1 |
… |
xn |
|
yi |
y0 |
y1 |
… |
yn |
т.е. ищутся приближенные значения y в узлах сетки.
Интегрируя уравнение на отрезке ![]() , получим
, получим
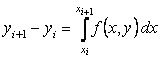
Вполне естественным (но не единственным) путем получения численного решения является замена в нем интеграла какой–либо квадратурной формулой численного интегрирования. Если воспользоваться простейшей формулой левых прямоугольников первого порядка
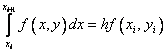 ,
,
то получим явную формулу Эйлера:
![]() ,
, ![]() .
.
Порядок расчетов:
Зная 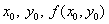 , находим
, находим 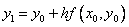 , затем
, затем 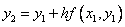 т.д.
т.д.
Геометрическая интерпретация метода Эйлера:
Пользуясь тем,
что в точке x0 известно решение y(x0) = y0
и значение его производной ![]() , можно записать уравнение касательной к
графику искомой функции
, можно записать уравнение касательной к
графику искомой функции ![]() в
точке
в
точке ![]() :
: ![]() . При достаточно малом
шаге h ордината
. При достаточно малом
шаге h ордината ![]() этой касательной, полученная подстановкой в
правую часть значения
этой касательной, полученная подстановкой в
правую часть значения ![]() ,
должна мало отличаться от ординаты y(x1) решения y(x) задачи Коши. Следовательно, точка
,
должна мало отличаться от ординаты y(x1) решения y(x) задачи Коши. Следовательно, точка 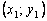 пересечения касательной с прямой x = x1
может быть приближенно принята за новую начальную точку. Через эту точку снова
проведем прямую
пересечения касательной с прямой x = x1
может быть приближенно принята за новую начальную точку. Через эту точку снова
проведем прямую ![]() ,
которая приближенно отражает поведение касательной к
,
которая приближенно отражает поведение касательной к 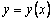 в точке
в точке 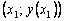 . Подставляя сюда
. Подставляя сюда ![]() (т.е. пересечение с
прямой x = x2), получим приближенное значение y(x) в точке x2:
(т.е. пересечение с
прямой x = x2), получим приближенное значение y(x) в точке x2: ![]() и т.д. В итоге для i–й
точки получим формулу Эйлера.
и т.д. В итоге для i–й
точки получим формулу Эйлера.
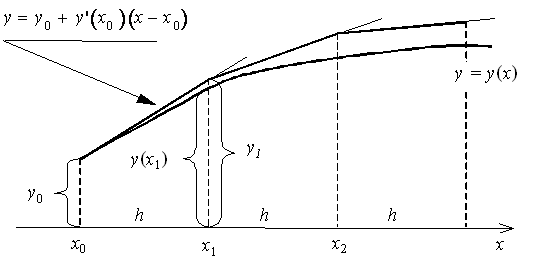
Явный метод Эйлера имеет первый порядок точности или аппроксимации.
Если использовать формулу правых прямоугольников: 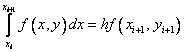 , то придем к методу
, то придем к методу
![]() ,
, 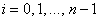 .
.
Этот метод называют неявным методом Эйлера,
поскольку для вычисления неизвестного значения ![]() по известному значению
по известному значению 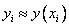 требуется решать уравнение, в общем
случае нелинейное.
требуется решать уравнение, в общем
случае нелинейное.
Неявный метод Эйлера имеет первый порядок точности или аппроксимации.
Модифицированный
метод Эйлера:
в
данном методе вычисление ![]() состоит
из двух этапов:
состоит
из двух этапов:

Данная схема называется еще методом предиктор – корректор (предсказывающее – исправляющее). На первом этапе приближенное значение предсказывается с невысокой точностью (h), а на втором этапе это предсказание исправляется, так что результирующее значение имеет второй порядок точности.
Методы Рунге – Кутта: идея построения явных методов Рунге–Кутты p–го порядка заключается в получении приближений к значениям y(xi+1) по формуле вида
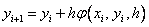 ,
,
где
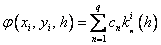
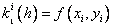
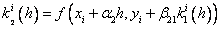
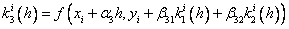
…………………………………………….
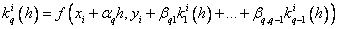 .
.
Здесь
an, bnj, pn, ![]() – некоторые фиксированные числа (параметры).
– некоторые фиксированные числа (параметры).
При построения методов
Рунге–Кутты параметры функции ![]() (an, bnj, pn) подбирают таким образом, чтобы получить
нужный порядок аппроксимации.
(an, bnj, pn) подбирают таким образом, чтобы получить
нужный порядок аппроксимации.
Схема Рунге – Кутта четвертого порядка точности:
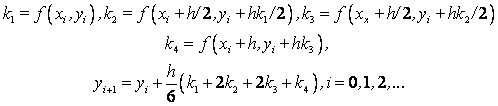
Пример. Решить задачу Коши:
![]() .
.
Рассмотреть три метода: явный метод Эйлера, модифицированный метод Эйлера, метод Рунге – Кутта.
Точное решение: ![]()
Расчетные формулы по явному методу Эйлера для данного примера:
![]()
Расчетные формулы модифицированного метода Эйлера:
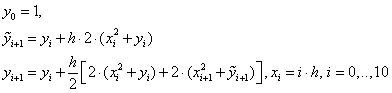
Расчетные формулы метода Рунге – Кутта:
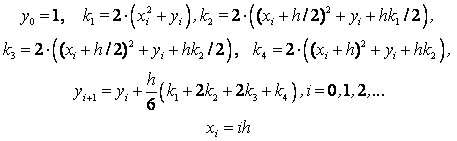
|
x |
y1 |
y2 |
y3 |
точное |
|
0 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
|
0.1 |
1.2000 |
1.2210 |
1.2221 |
1.2221 |
|
0.2 |
1.4420 |
1.4923 |
1.4977 |
1.4977 |
|
0.3 |
1.7384 |
1.8284 |
1.8432 |
1.8432 |
|
0.4 |
2.1041 |
2.2466 |
2.2783 |
2.2783 |
|
0.5 |
2.5569 |
2.7680 |
2.8274 |
2.8274 |
|
0.6 |
3.1183 |
3.4176 |
3.5201 |
3.5202 |
|
0.7 |
3.8139 |
4.2257 |
4.3927 |
4.3928 |
|
0.8 |
4.6747 |
5.2288 |
5.4894 |
5.4895 |
|
0.9 |
5.7377 |
6.4704 |
6.8643 |
6.8645 |
|
1 |
7.0472 |
8.0032 |
8.5834 |
8.5836 |
y1 – метод Эйлера, y2 – модифицированный метод Эйлера, y3 – метод Рунге Кутта.
Видно, что самым точным является метод Рунге – Кутта.
Рассмотренные методы могут быть использованы также для решения систем дифференциальных уравнений первого порядка.
Покажем это для случая системы двух уравнений первого порядка:

Явный метод Эйлера:
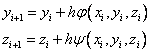
Модифицированный метод Эйлера:

Схема Рунге – Кутта четвертого порядка точности:

К решению систем уравнений ОДУ сводятся также задачи Коши для уравнений высших порядков. Например, рассмотрим задачу Коши для уравнения второго порядка
![]()
Введем вторую неизвестную функцию
![]() . Тогда задача
Коши заменяется следующей:
. Тогда задача
Коши заменяется следующей:

Т.е. в терминах предыдущей
задачи: ![]() .
.
Пример. Найти решение задачи Коши:
![]() на отрезке [0,1].
на отрезке [0,1].
Точное решение: ![]()
Действительно:

Решим задачу явным методом Эйлера, модифицированным методом Эйлера и Рунге – Кутта с шагом h=0.2.
Введем функцию ![]() .
.
Тогда получим следующую задачу Коши для системы двух ОДУ первого порядка:
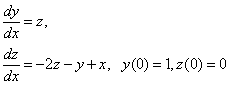
Явный метод Эйлера:
![]()
Модифицированный метод Эйлера:

Метод Рунге – Кутта:

Схема Эйлера:
|
X |
y |
z |
y теор |
z теор |
y-y теор |
|
0 |
1 |
0 |
1 |
0 |
0 |
|
0.2 |
1 |
-0.2 |
0.983685 |
-0.14622 |
0.016315 |
|
0.4 |
0.96 |
-0.28 |
0.947216 |
-0.20658 |
0.012784 |
|
0.6 |
0.904 |
-0.28 |
0.905009 |
-0.20739 |
0.001009 |
|
0.8 |
0.848 |
-0.2288 |
0.866913 |
-0.16826 |
0.018913 |
|
1 |
0.80224 |
-0.14688 |
0.839397 |
-0.10364 |
0.037157 |
Модифицированный метод Эйлера:
|
X |
ycv |
zcv |
y |
z |
y теор |
z теор |
y-y теор |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
0.2 |
1 |
-0.2 |
1 |
-0.18 |
0.983685 |
-0.14622 |
0.016315 |
|
0.4 |
0.96 |
-0.28 |
0.962 |
-0.244 |
0.947216 |
-0.20658 |
0.014784 |
|
0.6 |
0.904 |
-0.28 |
0.9096 |
-0.2314 |
0.905009 |
-0.20739 |
0.004591 |
|
0.8 |
0.848 |
-0.2288 |
0.85846 |
-0.17048 |
0.866913 |
-0.16826 |
0.008453 |
|
1 |
0.80224 |
-0.14688 |
0.818532 |
-0.08127 |
0.839397 |
-0.10364 |
0.020865 |
Схема Рунге - Кутта:
|
x |
Y |
z |
k1 |
l1 |
k2 |
l2 |
k3 |
l3 |
k4 |
l4 |
|
0 |
1 |
0 |
0 |
-1 |
-0.1 |
-0.7 |
-0.07 |
-0.75 |
-0.15 |
-0.486 |
|
0.2 |
0.983667 |
-0.1462 |
-0.1462 |
-0.49127 |
-0.19533 |
-0.27839 |
-0.17404 |
-0.31606 |
-0.20941 |
-0.13004 |
|
0.4 |
0.947189 |
-0.20654 |
-0.20654 |
-0.13411 |
-0.21995 |
0.013367 |
-0.2052 |
-0.01479 |
-0.2095 |
0.112847 |
|
0.6 |
0.904977 |
-0.20734 |
-0.20734 |
0.10971 |
-0.19637 |
0.208502 |
-0.18649 |
0.187647 |
-0.16981 |
0.27195 |
|
0.8 |
0.866881 |
-0.16821 |
-0.16821 |
0.269542 |
-0.14126 |
0.332455 |
-0.13497 |
0.317177 |
-0.10478 |
0.369665 |
|
1 |
0.839366 |
-0.1036 |
-0.1036 |
0.367825 |
-0.06681 |
0.40462 |
-0.06313 |
0.393583 |
-0.02488 |
0.423019 |
Max(y-y теор)=4*10-5
Постановка задачи: найти решение линейного дифференциального уравнения
![]() , (1)
, (1)
удовлетворяющего краевым
условиям:![]() . (2)
. (2)
Теорема. Пусть ![]() . Тогда существует
единственное решение поставленной задачи.
. Тогда существует
единственное решение поставленной задачи.
К данной задаче сводится, например, задача об определении прогибов балки, которая на концах опирается шарнирно.
Основные этапы метода конечных разностей:
1)
область непрерывного изменения аргумента ([a,b]) заменяется дискретным множеством точек, называемых
узлами: ![]() .
.
2)
Искомая функция непрерывного аргумента x,
приближенно заменяется функцией дискретного аргумента на заданной сетке, т.е. ![]() . Функция
. Функция ![]() называется сеточной.
называется сеточной.
3) Исходное дифференциальное уравнение заменяется разностным уравнением относительно сеточной функции. Такая замена называется разностной аппроксимацией.
Таким образом, решение дифференциального уравнения сводится к отысканию значений сеточной функции в узлах сетки, которые находятся из решения алгебраических уравнений.
Аппроксимация производных.
Для аппроксимации (замены) первой производной можно воспользоваться формулами:
![]() - правая разностная производная,
- правая разностная производная,
![]() - левая разностная производная,
- левая разностная производная,
![]() - центральная разностная производная.
- центральная разностная производная.
т.е., возможно множество способов аппроксимации производной.
Все эти определения следуют из
понятия производной как предела: ![]() .
.
Опираясь на разностную аппроксимацию первой производной можно построить разностную аппроксимацию второй производной:
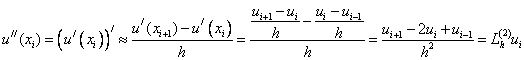 (3)
(3)
Аналогично можно получить аппроксимации производных более высокого порядка.
Определение. Погрешностью
аппроксимации n- ой производной называется разность: ![]() .
.
Для определения порядка аппроксимации используется разложение в ряд Тейлора.
Рассмотрим правую разностную аппроксимацию первой производной:
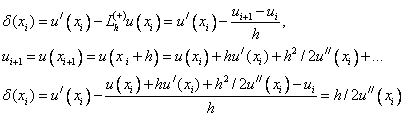
Т.е. правая разностная производная имеет первый по h порядок аппроксимации.
Аналогично и для левой разностной производной.
Центральная разностная производная имеет второй порядок аппроксимации.
Аппроксимация второй производной по формуле (3) также имеет второй порядок аппроксимации.
Для того чтобы аппроксимировать дифференциальное уравнение необходимо в нем заменить все производные их аппроксимациями. Рассмотрим задачу (1), (2) и заменим в(1) производные:
![]() .
.
В результате получим:
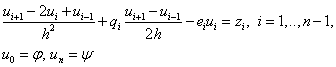 (4)
(4)
Порядок аппроксимации исходной задачи равен 2, т.к. вторая и первая производные заменены с порядком 2, а остальные – точно.
Итак, вместо дифференциальных
уравнений (1), (2) получена система линейных уравнений для определения ![]() в узлах сетки.
в узлах сетки.
Схему можно представить в виде:

т.е., получили систему линейных уравнений с матрицей:

Данная матрица является трехдиагональной, т.е. все элементы, которые расположены не на главной диагонали и двух прилегающих к ней диагоналях равны нулю.
Решая полученную систему уравнений, мы получим решение исходной задачи.
Для решения таких СЛАУ имеется экономичный метод прогонки.
Рассмотрим метод прогонки для СЛАУ:
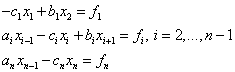 (1)
(1)
Решение данной системы ищем в виде:
![]() (2)
(2)
Подставляя в первое уравнение, получим:
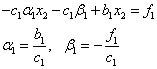
Здесь учтено, что данное
соотношение должно выполняться при любом ![]()
Так как
![]() , (3)
, (3)
то подставляя (3) во второе уравнение, получим:
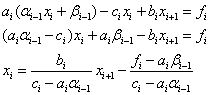
Сравнивая с (2) получим
![]() .
.
Таким образом, можно найти все ![]() .
.
Тогда из последнего уравнения (1) находим:
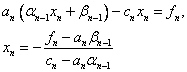
Затем последовательно находим:
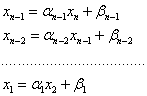
Таким образом, алгоритм метода прогонки можно представить в виде:
1) Находим
![]()
2) Для i=1,n-1: 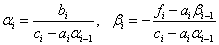 (4)
(4)
3) Находим
![]()
4) Для i=n-1 до 1 находим: ![]()
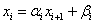
Шаги 1),2) – прямой ход метода прогонки, 3),4) – обратный ход метода прогонки.
Теорема. Пусть коэффициенты ai, bi системы уравнений при i =2, 3, …, n–1 отличны от нуля и пусть
![]() при i =1, 2, 3, …, n. Тогда прогонка
корректна и устойчива.
при i =1, 2, 3, …, n. Тогда прогонка
корректна и устойчива.
При выполнении этих условий знаменатели в алгоритме метода прогонки не обращаются в нуль и, кроме того, погрешность вычислений, внесенная на каком либо шаге вычислений, не будет возрастать при переходе к следующим шагам. Данное условие есть ни что иное, как условие диагонального преобладания.
Для нашей краевой задачи имеем :

Тогда: 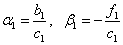 ,
, ![]() ,
,
![]()
Для нашей задачи условие устойчивости имеет вид:
![]() .
.
Пусть
![]() . (6)
. (6)
Тогда 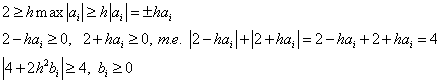
Пример. Найти решение задачи:
![]()
Выпишем разностную схему
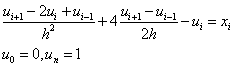
Условие устойчивости примет вид ![]()
Возьмем 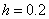 .
.
Тогда 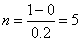
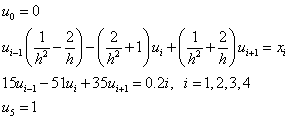
Или
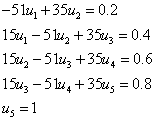
Формулы прогонки были получены для СЛАУ (1):
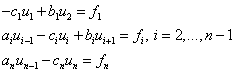
Здесь x замены на u.
Следовательно,
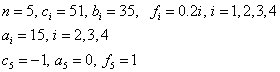
Решим СЛАУ методом прогонки. Вычисления оформим в виде таблицы:
|
I |
ai |
ci |
bi |
fi |
alfai |
betai |
ui |
|
1 |
|
51 |
35 |
0.2 |
0.6863 |
-0.0039 |
0.4701 |
|
2 |
15 |
51 |
35 |
0.4 |
0.8598 |
-0.0113 |
0.6906 |
|
3 |
15 |
51 |
35 |
0.6 |
0.9186 |
-0.0202 |
0.8164 |
|
4 |
15 |
51 |
35 |
0.8 |
0.9403 |
-0.0296 |
0.9107 |
|
5 |
0 |
-1 |
|
1 |
|
|
1.0000 |
Порядок вычислений по формулам (4):
![]()
![]()
![]()
![]()
Ответ в столбце ui.
Если забыли формулы, то их можно легко вывести. Главное запомнить основную формулу:
![]()
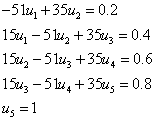
Прямой ход

Обратный ход
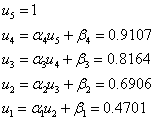
На практике часто граничные условия могут иметь более общий вид.
Рассмотрим следующую краевую задачу:
Найти решение ОДУ 2-го порядка
![]() ,
,
удовлетворяющую краевым условиям:
![]()
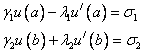
![]()
В этом случае при построении разностной схемы необходимо еще аппроксимировать и краевые условия.
Аппроксимация:
![]()
В результате получим разностную схему:
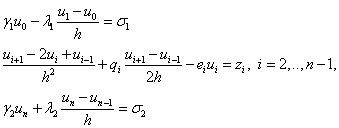
Или
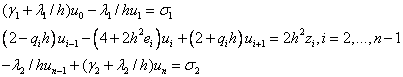
Мы получили СЛАУ типа (5) с трехдиагональной матрицей, решение которой также можно найти методом прогонки.
|
|